미생물의 화가, 알렉산더 플레밍

페니실린을 발견한 알렉산더 플레밍. 그는 젊은 시절부터 첼시 예술 클럽의 회원이었다. © Corbis

이 유명한 발견에는 더 흥미로운 뒷이야기가 있다. 플레밍이 푸른곰팡이의 항생작용을 발견한 것은 일정 부분 그의 취미 덕분이다. 플레밍은 과학자로서의 커리어를 시작하기 전부터 그림에 관심이 많았다. 그는 1890년 설립된 예술가 모임인 ‘첼시 예술 클럽’의 회원이자 아마추어 화가로서 수채화를 즐겨 그렸다. 이 취미가 어지간히 좋았던지, 플레밍은 미생물을 연구하기 시작한 이후로 특별한 재료를 써보기로 했다. 미생물을 이용해 페트리접시에 그림을 그린다는 아이디어였다. 

플레밍이 미생물로 배지에 그린 그림. 고유의 색소를 지닌 여러 종의 미생물을 접종하여 완성했다. 

© Alexander Fleming Laboratory Museum/Imperial College Healthcare NHs Trust

장난과 연구 사이, 클로드 섀넌

젊은 시절의 클로드 섀넌. 그는 거의 혼자서 현대 정보통신기술의 근간을 마련했다. © Estate of Francis Bello/Science Source

플레밍의 취미와 과학적 업적의 관계가 다소 막연한 짐작의 영역이라면, 클로드 섀넌(Claude Elwood Shannon)의 취미와 업적은 분명한 연관이 있다. 섀넌은 대중적으로는 생소하지만, 현대 과학기술을 이야기할 때 결코 빼놓을 수 없는 과학자다. 그의 업적은 단 한 문장으로 표현할 수 있다. “오늘날의 정보통신기술은 모두 섀넌으로부터 시작되었다.” 정보통신 분야의 영향력으로 따지면 Bill Gates나 Dennis Ritchie, 심지어는 오늘날 컴퓨터의 구조를 제시한 John von Neumann마저도 섀넌에 미치지 못한다.

섀넌의 중요한 업적 중 하나는 ‘불 게이트(Boolean gate)’를 이론적으로 설명한 것이다. 불 게이트는 19세기 중반 논리를 수학적으로 표현한 영국의 수학자인 조지 불(George Boole)에게서 따 온 이름이다. 불은 ‘참과 거짓’ 두 가지 값만으로 연산 가능한 수학적 체계를 구상하고, 이를 통해 논리를 수학 연산으로 표현했다. 섀넌은 불 대수의 두 가지 상태값인 참과 거짓을 ‘전류가 흐르는 상태와 흐르지 않는 상태’의 두 가지 전기 신호에 대응시켜, 입력된 신호에 따라 특정한 출력을 내는 ‘스위치’를 구상했다. 이러한 스위치를 불 게이트 또는 논리 게이트라고 한다. 이는 모든 논리적 진술을 전기적인 신호로 표현할 수 있음을 보여준다. 달리 말하면 세상의 모든 규칙을 전기 회로로 구현할 수 있다는 뜻으로, 즉 현대적인 의미에서 컴퓨터의 가능성을 암시한 것이다.

섀넌은 ‘디지털 혁명의 출생증명서’라고도 불리는 이 이론을, 그가 21살일 때 발표한 매사추세츠 공대(MIT) 석사학위 논문에서 다루었다. 섀넌의 업적은 여기서 그치지 않는다. 그는 2차 세계대전 동안 미국의 암호 분석팀에서 일하며 현대적인 대칭 블록 암호 알고리즘의 수학적 체계를 완성하여, ‘현대 암호학의 창시자’라고 불린다. 전쟁이 끝난 후에는 ‘정보통신의 수학적 이론’이라는 논문을 발표하여 디지털 통신 방식을 정립했다. ‘정보통신의 수학적 이론’은 전 세계의 모든 논문 중 인용 횟수가 4번째로 많을 만큼 중요한 논문이다. 요약하자면, 오늘날 스마트폰이 작동하는 데 필요한 핵심 요소인 컴퓨팅이나 암호화, 디지털 통신이 모두 섀넌의 발견에서 비롯된 셈이다.

섀넌의 여러 업적은 놀라울 만큼 시대를 앞서갔지만, 한편으로는 너무 급진적이라서 당대에는 과소평가 되곤 했다. 섀넌이 벨 연구소에 있을 때 동료였던 에드가 길버트(Edgar Gilbert)에 따르면, 섀넌이 내놓는 아이디어에 대해 연구소의 동료들은 흥미롭지만 그다지 유용하지는 않다는 반응을 보였다고 한다. 트랜지스터조차 없어 진공관을 게이트로 사용해야 하는 당시로서는, 섀넌의 아이디어를 실제로 구현할 하드웨어나 개념적인 틀이 없었기 때문이다. 섀넌이 제시한 개념의 진가가 드러나기 시작한 시기는 1970년대 초반, 집적회로가 등장하면서부터다.

그러나 정작 섀넌 자신은 이러한 현실의 한계에 전혀 개의치 않았던 것으로 보인다. 섀넌이 훗날 회고했듯, 그는 ‘항상 세상에 대한 가치를 고려하지 않고 제 관심사만 추구’했다. 그 대단한 업적도 그에게는 장난스러운 일에 몰두하다가 나온 아이디어였을 뿐이다. 만년의 섀넌은 역사상 가장 중요한 석사학위 논문으로 손꼽히는 그의 불 게이트 논문에 대한 인터뷰에서도, “늘 ‘불’이란 단어를 좋아했거든요.”라고만 언급했을 뿐이다.

순수한 흥밋거리와 진지한 연구가 뒤섞인 섀넌의 장난기는 벨 연구소에서부터 유명했다. 그는 외발자전거와 저글링에 취미를 붙여서 연구소의 복도를 저글링하며 질주하곤 했고, 나중에는 ‘저글링의 통합장 이론’을 만들어 냈다. 어떠한 상황에서도 안정적으로 저글링할 수 있는 물리적 해법을 구하는 이 이론은 B/H=(D+F)/(D+E)로 표현된다. 여기에서 B와 H는 각각 공과 손의 개수, D와 E 및 F는 각각 공이 한 손에 머무르는 시간, 각 손이 비어있는 시간, 각 공의 비행시간을 뜻한다. 이름부터 물리학의 ‘대통합이론’을 패러디한 이 수식은 그저 장난처럼 보이지만, 의외로 쓸모가 있었다. 무언가 뚝딱거리고 만드는 것을 좋아한 섀넌이 ‘저글링 기계’를 설계하는 데 이론적 기반이 된 것이다.

외발자전거를 타면서 저글링하는 클로드 섀넌. 저 모습 그대로 벨 연구소 복도를 돌아다녔다고 한다. © Courtesy of the Shannon family

섀넌은 이전에도 장난감 같은 기계를 발명한 적이 있다. ‘테세우스’라는 이름의 생쥐 로봇이다. 1950년에 만든 로봇이라서 미로가 놓인 테이블 아래에 덩치 큰 진공관 회로가 있고, 생쥐 로봇은 그저 자석이 이끄는 대로 따라가는 눈속임 같은 장치였다. 그렇지만 생쥐 로봇은 테세우스라는 이름처럼 미로의 벽을 따라 스스로 길을 찾을 수 있었다.

MIT 박물관에 전시된 섀넌의 테세우스. 쥐에 컴퓨터가 있는 것은 아니고, 미로 아래의 테이블 안에 거대한 진공관 연산장치가 있었다. © Daderot

테세우스가 세상에 널리 알려진 계기도 꽤 장난스럽다. 1977년 전기·전자 분야에서 가장 권위 있는 학회인 전기전자공학자협회(Institute of Electrical and Electronics Engineers, IEEE)가 미로에서 스스로 올바른 경로를 찾을 수 있는 ‘마이크로마우스’ 대회를 개최했다. 벨 연구소 시절 섀넌의 동료가 이 소식을 듣고는, IEEE에 연락하여 20여 년 전에 섀넌이 이미 그러한 종류의 마이크로마우스를 만들었다고 알려줬다. 트랜지스터도 없던 1950년대 기술로는 스스로 학습하는 생쥐 로봇이 불가능했으리라는 사실을 잘 알면서도, IEEE 측은 섀넌에게 연락했다. 섀넌은 폭소하면서 자신의 ‘속임수’에 대해 설명했다고 한다. 1979년 대회의 시상식에서 섀넌은 1950년의 그 생쥐 로봇을 싣고 와서 수상작들과 나란히 전시하기까지 했다.

1958년 벨 연구소를 떠나 MIT의 교수로 부임한 이후에, 섀넌은 자신만의 장난감에 깊이 빠져들었다. 섀넌은 자신만의 사색에 몰입하느라 강의에 통 열의가 없었다. 몇 학기가 지난 후에는 아예 학교 측에 더 이상 강의를 하지 않겠다고 통보하기까지 했다. 대단한 점은 MIT가 이를 이의 없이 받아들였다는 점이다. 강의에 대한 부담에서 벗어난 섀넌은 보스턴 교외의 집 지하실에 ‘장난감 방’을 차리고는, 여기서 오만가지 기계들을 만들었다. 불꽃을 쏘아올리는 트럼펫부터 로켓으로 회전하는 프리스비, 물 위를 걸을 수 있는 발포플라스틱 신발까지 하나같이 실용성이 의심스러운 물건들이었다. 개중에는 라스베이거스의 카지노에서 실제로 사용했던 도박용 웨어러블 컴퓨터처럼 애매하게 쓸모 있는 것도 있었지만, 섀넌은 대체로 ‘미친 과학자’의 스테레오타입에 들어맞는 일에 몰두했다. 이러한 활동 대부분은 자기만족을 위한 것이었지만, 끊임없는 창의성의 원천이기도 했다.

생산적 창조에 이르는 놀이

섀넌의 장난이 개인적이었다면, 그 후배들은 ‘공적인’ 장난으로 집단적 창의성을 자극하기도 했다. 장난스럽게 시작했으나 지금은 제법 어엿한 학습 도구로 발전한 양자 체스가 좋은 사례다.

근래 양자통신이니 양자컴퓨팅이니 하는 단어가 여기저기 오르내리지만, 이를 제대로 이해하기는 쉽지 않다. 양자 기술은 흔히 우리가 지각하는 물리 세계의 직관으로는 이해하기 어려운 양자적 ‘기묘함’에 바탕을 두기 때문이다. 대표적인 성질이 바로 ‘중첩’이다. 중첩은 같은 시간, 같은 위치에서 여러 가지 상태로 존재하는 것을 말한다. 흔히 ‘슈뢰딩거의 고양이’로 비유되곤 하는데, 고양이가 죽어있는 동시에 살아있는 말도 안 되는 상황이다. 여기에서 얽힘이나 관찰자 효과까지 나아가면, 분명 우리말로 쓰여있는데 내용은 도통 이해할 수 없는 지경에 이르고 만다.

이를 알기 쉽게 설명하는 방법은 없을까? 일단 슈뢰딩거의 고양이는 별로 도움이 되지 않는다. 애초에 양자적 중첩 개념이 말도 안 된다고 비판하고자 든 예시인 데다, ‘양자 세계가 이렇게 이상합니다.’라는 메시지밖에 없기 때문이다. 그렇다면 누구나 알 만한 게임에 양자적 기묘함을 적용해 본다면 어떨까?

이런 아이디어에서 출발한 것이 양자 체스다. 퀸즈대학교(Queen’s University)의 교수인 셀림 아클(Selim Akl)과 그의 제자인 앨리스 위스매스(Alice Wismath)는 체스에 양자적 예측 불가능성을 도입해 실행 가능한 게임으로 구현했다. 사실 양자 체스를 고안한 계기는 약간 치사했다. 컴퓨터가 인간을 상대로 체스에서 완전한 우위를 점한 이후, ‘사람이 다시 기계를 이기려면 체스 룰을 어떻게 바꾸는 것이 좋을까’라는 고민이 그 계기였다. 치사하다고 표현하기는 했지만, 물론 학술적으로는 중요한 의미가 있었다. 체스 컴퓨터에 적용된 전통적인 가지치기 알고리즘으로는 구현할 수 없는, 새로운 알고리즘을 탐색한다는 의미가 있었으니까.

양자 체스의 기본 세팅은 전통적인 체스와 동일하다. 다만 킹을 제외한 모든 말이 중첩 상태 또는 이미 확정된 상태 중 하나를 선택하여 시작해야 한다는 점이 다르다. 중첩 상태의 말은 플레이어가 손을 대는 즉시 두 가지 가능한 상태 중 하나로 고정된다. 이는 ‘중첩 상태의 양자는 외부와 상호작용하는 순간 중첩 상태가 붕괴되고 특정 상태로 고정된다.’라는 ‘관찰자 효과’를 표현한 것이다.

양자 체스의 기본 세팅. 킹을 제외한 모든 말은 원래의 말과 또 다른 말의 중첩된 상태로 존재한다. © Queen‘s University, California

임페리얼 칼리지 런던(Imperial College London)의 크리스 캔트웰(Chris Cantwell)은 양자 체스의 룰을 한층 복잡하게 꼬아놓았다. 중첩은 입자가 움직이는 상태와 정지한 상태가 동시에 나타나는 것이다. 따라서 말을 중첩된 상태로 유지하고 이동시킨다면, 이동한 체스판과 이동하지 않은 체스판 두 가지 모두에 형세가 중첩되어 존재할 수 있다. 만약 중첩된 말 두 개가 하나의 칸에 들어간다면, 각 말의 중첩 확률에 따라 어느 말이 남을지 결정된다. 그에 따라 다른 말의 위치도 연쇄적으로 영향을 받는다.

위치의 중첩 상태를 보여주는 사례. B8의 흑색 나이트는 이동하기 전 100% 확률로 한 위치에 존재한다(왼쪽). 그러나 두 번 움직여 D4로 이동한 상태에서는 원래의 B8과 이동한 D4, 두 위치가 중첩된 상태로 있는다(오른쪽). © Chess Stackexchange

어딘가 더 모를듯한 이야기가 되는 것 같지만, 그러려니 하자. 양자 체스는 실제 체스판에서 다루기에는 원체 복잡하니까. 다만 프로그램의 구조를 몰라도 컴퓨터 게임을 즐기는 데에는 아무 문제가 없듯, 세세한 룰은 잊어버리고 컴퓨터의 힘을 빌어서 게임에 뛰어드는 것은 가능하다. 요약하자면, 양자 체스는 전형적인 결정론적 세계인 고전 체스에 확률을 도입하여 난장판으로 만든 체스다. 아클과 위스매스, 캔트웰이 진지한 학술적 탐구 이전에, ‘체스 룰에 양자적 특성을 도입해 보면 재미있지 않을까?’하는 생각에서 출발한 것이 양자 체스니까.

장난스럽게 시작했으나 게임의 틀을 활용한 덕분에, 양자 체스는 양자적 기묘함을 직관적으로 전달할 수 있었다. 놀이 과정에서 부딪히는 다양한 상황을 해결하면서 비직관적인 양자적 특성을 체득할 수 있는 것이다. 양자 체스는 게임 플랫폼인 ‘스팀’에도 얼리-액세스로 올라가 있으니 실제로 체험해 보기는 어렵지 않다. 다만, 인공지능이 부실한 데다 4년이 넘도록 얼리-액세스 꼬리표를 떼지 못하여 평이 좋지 않다는 점은 감안해야 한다.

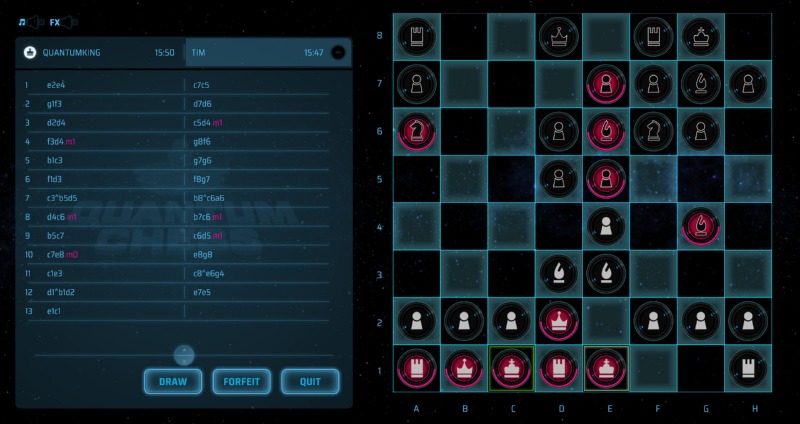
스팀에 올라온 버전의 양자 체스. 애석하게도 게임적 완성도에 문제가 있어서 평은 별로 좋지 않다. © Quantum Realm Games

플레밍의 미생물 그림부터 섀넌의 놀이방, 그리고 양자 체스에 이르기까지 저명한 과학자들은 늘 진지한 연구와 가벼운 놀이 사이를 넘나들며 업적을 쌓아 왔다. 사실 연구와 놀이 자체가 구분되지 않는, ‘중첩된’ 상태라고 보는 것이 맞을 것이다. 사람들은 흔히 취미를 ‘일 이외의 무언가’로 생각하는 경향이 있지만, 지적으로 생산적인 사람일수록 취미의 우선순위가 높다는 사실에 주목해야 한다. 호기심이야말로 생산적인 지적 활동의 원동력이고, 그 호기심을 자극하는 데 가장 좋은 것이 사심 없이 즐기는 놀이이다.